Bayes Teorisi: Koşullu olasılığı belirleme formülü haberi

Bayes Teoremi nedir? Bayes Teorisi nedir? Koşullu olasılık nasıl belirlenir?

Bayes Teoremi; olasılığa dayalı sınıflandırma yöntemidir. Koşullu olasılıktan yararlanan Bayes Teoremi bir sonucun sebebini ararken, sonucun hangi olasılıklarla, hangi sebeplerden kaynaklanmış olabileceğini bulmaya yardımcı olur.

Formül; P(A|B) = P(B|A) . P(A) / P(B) şeklindedir.

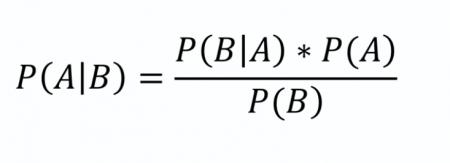
Formülde;

P(A|B) = B olayı gerçekleştiğinde A olayının gerçekleşme olasılığı
P(A) = A olayının gerçekleşme olasılığı
P(B|A) = A olayı gerçekleştiğinde B olayının gerçekleşme olasılığı
P(B) = B olayının gerçekleşme olasılığını ifade eder.

Olasılık teorileri arasında en yaygın kullanılan teoridir. Adını 18. yüzyılda yaşayan İngiliz matematikçisi Thomas Bayes’den alan teorem, koşullu olasılığı belirlemek için kullanılan matematiksel formüldür.

Rormülün nasıl oluşturulduğu şu şekilde izah edilir:

Koşullu olasılık kuralına göre:

P(A|B) = P(A ve B) / P(B)

. Aynı şekilde :

P(B|A) = P(B ve A) / P(A)

P(A ve B) = P(B ve A)

Yukarıdaki iki denklemi birleştirirsek.

P(A|B).P(B)=P(B|A).P(A) buradan Bayes kuralını çıkarabilir.

P(A|B) = P(B|A) . P(A) / P(B)

Örnek

Araştırmaya göre her 43 çocuktan 1 tanesi, yetişkinlikte ortaya çıkan belli bir hastalığa yakalanmakta ve tam güvenilir olmamasına rağmen yapılan test sonuçlarına göre, hastalıklı bir çocuğun testi %80 pozitif, sağlıklı bir çocuğun testi ise %10 pozitif sonuç vermektedir. Bu bilgilere göre test sonucu pozitif olan bir çocuğun gerçekten hasta olma olasılığı nedir?

P(A) : Çocuğun hasta olması olasılığı = 1/43
P(B) : Testin pozitif çıkması olasılığı = 1/43 * 0.80 + 42/43 * 0.10 = 5/43
P(A|B) : Pozitif çıkan testin hastalık çıkma olasılığı ( sorulan bu )
P(B|A) : Hastalıklı çocuğun testinin pozitif çıkma olasılığı = 0.80

P(A|B)=P(B|A)*P(A)/P(B) => (0.80 * 1/43) / (5/43) = 0.16 = %16 bulunur.

Ali kaşındığını söylüyor. Kedi alerjisi için bir test var, ancak bu test her zaman doğru değil: Gerçekten alerjisi olan insanlar için, testin “Evet” sonucu vermesi %80 oranında. Alerjisi olmayan insanlar için, testin “Evet” sonucu vermesi %10 oranında (“false positive “). Nüfusun %1’inde alerji varsa ve test “Evet” çıkıyorsa, Ali’nin gerçekten alerji olma olasılığı nedir?

A: Alerji, B: Testin Evet çıkması
P(A) : Alerji olasılığı = 0.01
P(B) : Testin evet çıkma olasılığı = ? (hesaplamamız gerekecek)
P(A|B) : Testin evet çıkması durumunda alerji olasılığı = ?? (istenen sonuç)
P(B|A) : Alerji olması durumunda testin evet çıkma olasılığı = 0.80

Önce P(B) yi bulunur. Testin evet çıkma olasılığını alerjisi olan ve olmayanlar için yani tüm nüfus için hesaplanır.

P(B) = 0.01 * 0.80 + 0.99 * 0.10 = 0.107 bulduk.

Tüm verileri denkleme yerleştirilip sonuca gidilir:

P(A|B)=P(A)*P(B|A)/P(B) => 0.01 * 0.80 / 0.107 = 0.075 => yaklaşık %7 bulunur.

Özel Versiyon Formülasyonu ile teori birden çok olay için de kullanabilir.

Bir B olayının birbiriyle ayrık A olaylarından(A1,A2,A3,…,An) biriyle birlikte gerçekleşebileceği varsayalırsa, Bayes denklemi şöyle yazılabilir:

P(Ax|B) = P(Ax ve B) / ( P(A1 ve B) + P(A2 ve B)+ ..... P(An ve B) )

Çarpma kuralına göre teoriyi bu kez aşağıdaki gibi yazılır

Çarpma Kuralı : P(A ve B)= P(A) P(B|A)

Çarpma kuralı uygulanan Bayes formülü:

Yani iki ayrık A1 ve A2 olayları söz konusu ise Bayes formülü şöyle özelleştirebilir: